Projectile Motion

Projectile Motion

Horizontally Launched Projectile Problems

One of the powers of physics is its ability to use physics principles to make predictions about the final outcome of a moving object. Such predictions are made through the application of physical principles and mathematical formulas to a given set of initial conditions. In the case of projectiles, a student of physics can use information about the initial velocity and position of a projectile to predict such things as how much time the projectile is in the air and how far the projectile will go. The physical principles that must be applied are those discussed previously in Lesson 2. The mathematical formulas that are used are commonly referred to as kinematic equations. Combining the two allows one to make predictions concerning the motion of a projectile. In a typical physics class, the predictive ability of the principles and formulas are most often demonstrated in word story problems known as projectile problems.
There are two basic types of projectile problems that we will discuss in this course. While the general principles are the same for each type of problem, the approach will vary due to the fact the problems differ in terms of their initial conditions. The two types of problems are:

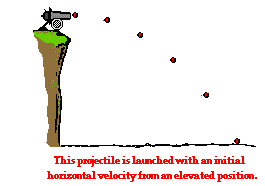Problem Type 1:

A projectile is launched with an initial horizontal velocity from an elevated position and follows a parabolic path to the ground. Predictable unknowns include the initial speed of the projectile, the initial height of the projectile, the time of flight, and the horizontal distance of the projectile.
Examples of this type of problem are

1. A pool ball leaves a 0.60-meter high table with an initial horizontal velocity of 2.4 m/s. Predict the time required for the pool ball to fall to the ground and the horizontal distance between the table's edge and the ball's landing location.
2. A soccer ball is kicked horizontally off a 22.0-meter high hill and lands a distance of 35.0 meters from the edge of the hill. Determine the initial horizontal velocity of the soccer ball.

Problem Type 2:
A projectile is launched at an angle to the horizontal and rises upwards to a peak while moving horizontally. Upon reaching the peak, the projectile falls with a motion that is symmetrical to its path upwards to the peak. Predictable unknowns include the time of flight, the horizontal range, and the height of the projectile when it is at its peak.
Examples of this type of problem are

1. A football is kicked with an initial velocity of 25 m/s at an angle of 45-degrees with the horizontal. Determine the time of flight, the horizontal distance, and the peak height of the football.
2. A long jumper leaves the ground with an initial velocity of 12 m/s at an angle of 28-degrees above the horizontal. Determine the time of flight, the horizontal distance, and the peak height of the long-jumper.

The second problem type will be the subject of the next part of Lesson 2. In this part of Lesson 2, we will focus on the first type of problem - sometimes referred to as horizontally launched projectile problems. Three common kinematic equations that will be used for both type of problems include the following:

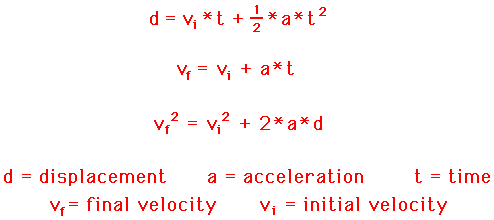
Equations for the Horizontal Motion of a Projectile

The above equations work well for motion in one-dimension, but a projectile is usually moving in two dimensions - both horizontally and vertically. Since these two components of motion are independent of each other, two distinctly separate sets of equations are needed - one for the projectile's horizontal motion and one for its vertical motion. Thus, the three equations above are transformed into two sets of three equations. For the horizontal components of motion, the equations are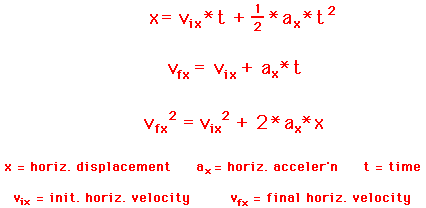
Of these three equations, the top equation is the most commonly used. An application of projectile concepts to each of these equations would also lead one to conclude that any term with a_x in it would cancel out of the equation since a_x = 0 m/s/s.

Equations for the Vertical Motion of a Projectile

For the vertical components of motion, the three equations are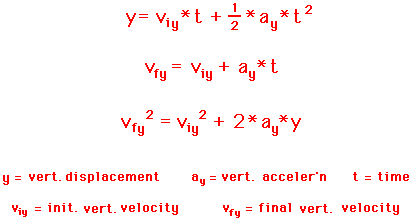
In each of the above equations, the vertical acceleration of a projectile is known to be -9.8 m/s/s (the acceleration of gravity). Furthermore, for the special case of the first type of problem (horizontally launched projectile problems), v_iy = 0 m/s. Thus, any term with v_iy in it will cancel out of the equation.
The two sets of three equations above are the kinematic equations that will be used to solve projectile motion problems.

Solving Projectile Problems

To illustrate the usefulness of the above equations in making predictions about the motion of a projectile, consider the solution to the following problem.

Example A pool ball leaves a 0.60-meter high table with an initial horizontal velocity of 2.4 m/s. Predict the time required for the pool ball to fall to the ground and the horizontal distance between the table's edge and the ball's landing location.

The solution of this problem begins by equating the known or given values with the symbols of the kinematic equations - x, y, v_ix, v_iy, a_x, a_y, and t. Because horizontal and vertical information is used separately, it is a wise idea to organized the given information in two columns - one column for horizontal information and one column for vertical information. In this case, the following information is either given or implied in the problem statement:

Horizontal Information	Vertical Information
x = ??? vix = 2.4 m/s ax = 0 m/s/s	y = -0.60 m viy = 0 m/s ay = -9.8 m/s/s

As indicated in the table, the unknown quantity is the horizontal displacement (and the time of flight) of the pool ball. The solution of the problem now requires the selection of an appropriate strategy for using the kinematic equations and the known information to solve for the unknown quantities. It will almost always be the case that such a strategy demands that one of the vertical equations be used to determine the time of flight of the projectile and then one of the horizontal equations be used to find the other unknown quantities (or vice versa - first use the horizontal and then the vertical equation). An organized listing of known quantities (as in the table above) provides cues for the selection of the strategy. For example, the table above reveals that there are three quantities known about the vertical motion of the pool ball. Since each equation has four variables in it, knowledge of three of the variables allows one to calculate a fourth variable. Thus, it would be reasonable that a vertical equation is used with the vertical values to determine time and then the horizontal equations be used to determine the horizontal displacement (x). The first vertical equation (y = v_iy•t +0.5•a_y•t²) will allow for the determination of the time. Once the appropriate equation has been selected, the physics problem becomes transformed into an algebra problem. By substitution of known values, the equation takes the form of

-0.60 m = (0 m/s)•t + 0.5•(-9.8 m/s/s)•t²

Since the first term on the right side of the equation reduces to 0, the equation can be simplified to

-0.60 m = (-4.9 m/s/s)•t²

If both sides of the equation are divided by -5.0 m/s/s, the equation becomes

0.122 s² = t²

By taking the square root of both sides of the equation, the time of flight can then be determined.

t = 0.350 s (rounded from 0.3499 s)

Once the time has been determined, a horizontal equation can be used to determine the horizontal displacement of the pool ball. Recall from the given information, v_ix = 2.4 m/s and a_x = 0 m/s/s. The first horizontal equation (x = v_ix•t + 0.5•a_x•t²) can then be used to solve for "x." With the equation selected, the physics problem once more becomes transformed into an algebra problem. By substitution of known values, the equation takes the form of

x = (2.4 m/s)•(0.3499 s) + 0.5•(0 m/s/s)•(0.3499 s)²

Since the second term on the right side of the equation reduces to 0, the equation can then be simplified to

x = (2.4 m/s)•(0.3499 s)

Thus,

x = 0.84 m (rounded from 0.8398 m)

The answer to the stated problem is that the pool ball is in the air for 0.35 seconds and lands a horizontal distance of 0.84 m from the edge of the pool table.

 

The following procedure summarizes the above problem-solving approach.

1. Carefully read the problem and list known and unknown information in terms of the symbols of the kinematic equations. For convenience sake, make a table with horizontal information on one side and vertical information on the other side.
2. Identify the unknown quantity that the problem requests you to solve for.
3. Select either a horizontal or vertical equation to solve for the time of flight of the projectile.
4. With the time determined, use one of the other equations to solve for the unknown. (Usually, if a horizontal equation is used to solve for time, then a vertical equation can be used to solve for the final unknown quantity.)

One caution is in order. The sole reliance upon 4- and 5-step procedures to solve physics problems is always a dangerous approach. Physics problems are usually just that - problems! While problems can often be simplified by the use of short procedures as the one above, not all problems can be solved with the above procedure. While steps 1 and 2 above are critical to your success in solving horizontally launched projectile problems, there will always be a problem that doesn't fit the mold. Problem solving is not like cooking; it is not a mere matter of following a recipe. Rather, problem solving requires careful reading, a firm grasp of conceptual physics, critical thought and analysis, and lots of disciplined practice. Never divorce conceptual understanding and critical thinking from your approach to solving problems.